Join the Numo Field Theory Community
Connect with researchers in focused chat rooms
The NUMO Field
A discrete reversible dynamical system on ten states with toroidal topology
Explore a symbolic framework built on four layers, reversible operators, and emergent cycles spanning applications from quantum pedagogy to oracle systems.
The Journey from Linear to Circular
The traditional linear number line has been humanity's primary tool for understanding numerical relationships for centuries. Its simplicity revealed fundamental patterns—symmetries, periodic intervals, and dual relationships— that ultimately pointed toward a deeper geometric truth.
📐The Linear Foundation: A Discovery Tool
The linear number line was essential to the discovery process. By arranging digits 0–9 in sequence, early observations revealed patterns that traditional mathematics had not fully explored:
- Dual-sum relationships: Placing digits linearly made it visible that certain pairs sum to 11 (2+9, 3+8, 4+7, 5+6), suggesting a hidden symmetry around a midpoint.
- Distance and reflection: The linear arrangement revealed mirror symmetries— digits equidistant from the center exhibited complementary properties.
- Sequential patterns: The linear form made it easy to observe cycles, especially the recurring pattern of 2→5→6→9, which later became the "engine ring."
- Boundary awareness: The endpoints (0 and 1) stood apart from the rest, hinting at a special interior/exterior relationship that the line couldn't fully capture.
These observations, only possible through linear visualization, revealed that the structure was trying to curve back on itself. The linear number line served as the conceptual scaffolding that made the circular transformation both discoverable and inevitable.
∞Mathematical Advantages Discovered Through Linear Analysis
- Closure under operators: Linear dual-sums (n+11-n) revealed perfect symmetry, leading to reversible δ operation
- Natural periodicity: The 2→5→6→9 cycle observed linearly becomes a continuous loop in circular form
- Reversibility: Mirror symmetries in linear space translate to exact inversions (μ operator) in the torus
- Symmetry groups: Linear distances revealed dihedral D₈ structure, formalized in circular geometry
- Dual relationships: The linear arrangement made $$n + \delta(n) = 11$$ pairings visually obvious
◉Conceptual Breakthroughs Enabled by Circular Form
- No endpoints: Linear boundaries disappeared, revealing continuous flow and cycles
- Interior/exterior duality: The "special" position of 0 and 1 now understood as central axis
- Layered organization: Linear distances became radial layers with distinct topological roles
- Twist and inversion: Membrane band (3,8) enables transformations impossible in linear space
- Visual intuition: Circular arrangement made digit shape symmetries (6↔9, 2↔5) geometrically meaningful
The Transformation Process
Traditional Linear Number Line
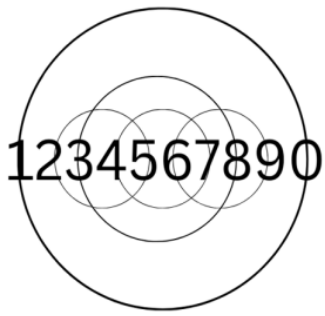
The Foundation: Linear representation revealed patterns in distances, symmetries, and dual relationships that made the circular structure discoverable
NUMO Circular Field
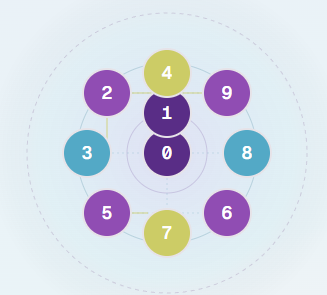
The Realization: Toroidal geometry with interior (0,1), membrane (3,8), axis (4,7), and engine ring (2,5,6,9) now fully expressing the latent structure
Why the Transformation Was Necessary
The linear number line was indispensable for discovery—it made patterns visible and relationships measurable. However, those very patterns revealed that the linear form was incomplete:
- • Cycles couldn't close without artificial "wrapping" or modular arithmetic
- • Dual pairs appeared symmetric but had no geometric reason for their relationship
- • Interior states (0,1) seemed different but had no structural explanation
- • Reversible operations felt constrained by endpoints and directionality
The circular NUMO Field doesn't replace the linear number line— it fulfills the patterns that linear representation revealed but couldn't fully express.
Dimensional Evolution: Line → Circle → Torus → Sphere
The NUMO Field's structure emerges through progressive dimensional transformations, each revealing new properties impossible in lower dimensions.
1D Linear Sequence
Digits arranged sequentially on a line. Patterns visible but endpoints constrain.
Dimensional Breakthroughs
Endpoints join. Cycles close naturally without artificial wrapping.
Layers gain topological meaning. Interior/exterior becomes structural.
Complete field unifies as discrete symbolic manifold with operator algebra.
Core Architecture
Interior Layer
The Cauldron states (0, 1) form the central cavity, mediating inside-outside transitions via the C operator.
Membrane Layer
The inversion band where twist events occur. Dual and mirror operators coincide here.
Axis Layer
Stabilizing vertical rails that anchor polarity and preserve orientation through transformations.
Engine Layer
The 4-cycle circulation ring. The L operator drives reversible motion around the torus.
Reversible Operators
All transformations in the NUMO Field are generated by four fundamental operators
Dual (δ)
$$n + \delta(n) = 11$$
Mirror (μ)
Left-right reflection
Cauldron (C)
Interior/exterior toggle
Loop (L)
$$2 \rightarrow 5 \rightarrow 6 \rightarrow 9$$
Application Spectrum
From definite implementations to speculative research directions
Dive Into the Theory
Explore the complete mathematical framework: axioms, operators, toroidal geometry, emergent behavior, and applications.
The NUMO Field: A Discrete Reversible Dynamical System
Christopher G. Phillips (Raziel Ali) • 2025
NUMO Field Application Spectrum
AvailableChristopher G. Phillips (Raziel Ali) • 2025